BCH code

In [[codin15}}). We will consider different values of }} its minimal polynomial over is

m_1(x) = x^4+x+1.

The minimal polynomials of the first fourteen powers of are

m_1(x) = m_2(x) = m_4(x) = m_8(x) = x^4+x+1,,

m_3(x) = m_6(x) = m_9(x) = m_{12}(x) =x^4+x^3+x^2+x+1,,

m_5(x) = m_{10}(x) = x^2+x+1,,

m_7(x) = m_{11}(x) = m_{13}(x) = m_{14}(x) = x^4+x^3+1.,

The BCH code with $d=2,3$ has generator polynomial

$g(x) = m_1(x) = x^4+x+1.,$

It has minimal at least 3 and corrects up to one error. Since the generator polynomial is of degree 4, this code has 11 data bits and 4 checksum bits.

The BCH code with $d=4,5$ has generator polynomial

$g(x) = {rm lcm}(m_1(x),m_3(x)) = (x^4+x+1)(x^4+x^3+x^2+x+1) = x^8+x^7+x^6+x^4+1.,$

It has minimal Hamming distance at least 5 and corrects up to two errors. Since the generator polynomial is of degree 8, this code has 7 data bits and 8 checksum bits.

The BCH code with $d=6,7$ has generator polynomial

$begin{align} g(x) & {} = {rm lcm}(m_1(x),m_3(x),m_5(x)) & {} = (x^4+x+1)(x^4+x^3+x^2+x+1)(x^2+x+1) & {} = x^{10}+x^8+x^5+x^4+x^2+x+1. end{align}$

It has minimal Hamming distance at least 7 and corrects up to three errors. Since the generator polynomial is of degree 10, this code has 5 data bits and 10 checksum bits.
(This particular generator polynomial has a real-world application, in the format patterns of the .)

The BCH code with $d=8$ and higher has generator polynomial

$begin{align} g(x) & {} = {rm lcm}(m_1(x),m_3(x),m_5(x),m_7(x)) & {} = (x^4+x+1)(x^4+x^3+x^2+x+1)(x^2+x+1)(x^4+x^3+1) & {} = x^{14}+x^{13}+x^{12}+cdots+x^2+x+1. end{align}$

This code has minimal Hamming distance 15 and corrects 7 errors. It has 1 data bit and 14 checksum bits. In fact, this code has only two codewords: 000000000000000 and 111111111111111.

1 General BCH codes
2 Special cases
3 Properties
4 Encoding
5 Decoding
6 Citations
7 Source
8 See Also on BitcoinWiki

General BCH codes

General BCH codes differ from primitive narrow-sense BCH codes in two respects.

First, the requirement that $alpha$ be a primitive element of $mathrm{GF}(q^m)$ can be relaxed. By relaxing this requirement, the code length changes from $q^m - 1$ to $mathrm{ord}(alpha),$ the of the element $alpha.$

Second, the consecutive roots of the generator polynomial may run from $alpha^c,ldots,alpha^{c+d-2}$ instead of $alpha,ldots,alpha^{d-1}.$

Definition. Fix a finite field $GF(q),$ where $q$ is a prime power. Choose positive integers $m,n,d,c$ such that $2leq dleq n,$ ${rm gcd}(n,q)=1,$ and $m$ is the of $q$ modulo $n.$

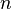As before, let $alpha$ be a primitive $n$ th root of unity in $GF(q^m),$ and let $m_i(x)$ be the over $GF(q)$ of $alpha^i$ for all $i.$ The generator polynomial of the BCH code is defined as the $g(x) = {rm lcm}(m_c(x),ldots,m_{c+d-2}(x)).$

Note: if $n=q^m-1$ as in the simplified definition, then ${rm gcd}(n,q)$ is 1, and the order of $q$ modulo $n$ is $m.$ Therefore, the simplified definition is indeed a special case of the general one.

Special cases

A BCH code with $c=1$ is called a narrow-sense BCH code.
A BCH code with $n=q^m-1$ is called primitive.

The generator polynomial $g(x)$ of a BCH code has coefficients from $mathrm{GF}(q).$ In general, a cyclic code over $mathrm{GF}(q^p)$ with $g(x)$ as the generator polynomial is called a BCH code over $mathrm{GF}(q^p).$ The BCH code over $mathrm{GF}(q^m)$ with $g(x)$ as the generator polynomial is called a . In other words, a Reed–Solomon code is a BCH code where the decoder alphabet is the same as the channel alphabet.

Properties

The generator polynomial of a BCH code has degree at most $(d-1)m$ . Moreover, if $q=2$ and $c=1$ , the generator polynomial has degree at most $dm/2$ .

Each minimal polynomial $m_i(x)$ has degree at most $m$ . Therefore, the least common multiple of $d-1$ of them has degree at most $(d-1)m$ . Moreover, if $q=2,$ then $m_i(x) = m_{2i}(x)$ for all $i$ . Therefore, $g(x)$ is the least common multiple of at most $d/2$ minimal polynomials $m_i(x)$ for odd indices $i,$ each of degree at most $m$ .

A BCH code has minimal Hamming distance at least $d$ .

Suppose that $p(x)$ is a code word with fewer than $d$ non-zero terms. Then

p(x) = b_1x^{k_1} + cdots + b_{d-1}x^{k_{d-1}},text{ where }k_1<k_2<cdots<k_{d-1}.

Recall that $alpha^c,ldots,alpha^{c+d-2}$ are roots of $g(x),$ hence of $p(x)$ . This implies that $b_1,ldots,b_{d-1}$ satisfy the following equations, for each $i in {c, dotsc, c+d-2}$ :

p(alpha^i) = b_1alpha^{ik_1} + b_2alpha^{ik_2} + cdots + b_{d-1}alpha^{ik_{d-1}} = 0.

In matrix form, we have

begin{bmatrix} alpha^{ck_1} & alpha^{ck_2} & cdots & alpha^{ck_{d-1}} alpha^{(c+1)k_1} & alpha^{(c+1)k_2} & cdots & alpha^{(c+1)k_{d-1}} vdots & vdots && vdots alpha^{(c+d-2)k_1} & alpha^{(c+d-2)k_2} & cdots & alpha^{(c+d-2)k_{d-1}} end{bmatrix} begin{bmatrix} b_1 \ b_2 \ vdots \ b_{d-1} end{bmatrix} = begin{bmatrix} 0 \ 0 \ vdots \ 0 end{bmatrix}.

The determinant of this matrix equals

left(prod_{i=1}^{d-1}alpha^{ck_i}right)detbegin{pmatrix} 1 & 1 & cdots & 1 alpha^{k_1} & alpha^{k_2} & cdots & alpha^{k_{d-1}} vdots & vdots && vdots alpha^{(d-2)k_1} & alpha^{(d-2)k_2} & cdots & alpha^{(d-2)k_{d-1}} end{pmatrix} = left(prod_{i=1}^{d-1}alpha^{ck_i}right) det(V).

The matrix $V$ is seen to be a , and its determinant is

det(V) = prod_{1le i<jle d-1} (alpha^{k_j}-alpha^{k_i}),

which is non-zero. It therefore follows that $b_1,ldots,b_{d-1}=0,$ hence $p(x)=0.$

A BCH code is cyclic. A polynomial code of length $n$ is cyclic if and only if its generator polynomial divides $x^n-1.$ Since $g(x)$ is the minimal polynomial with roots $alpha^c,ldots,alpha^{c+d-2},$ it suffices to check that each of $alpha^c,ldots,alpha^{c+d-2}$ is a root of $x^n-1.$ This follows immediately from the fact that $alpha$ is, by definition, an $n$ th root of unity.

Encoding

Decoding

There are many algorithms for decoding BCH codes. The most common ones follow this general outline:

Calculate the syndromes s_j for the received vector
Determine the number of errors t and the error locator polynomial Λ(x) from the syndromes
Calculate the roots of the error location polynomial to find the error locations X_i
Calculate the error values Y_i at those error locations
Correct the errors

During some of these steps, the decoding algorithm may determine that the received vector has too many errors and cannot be corrected. For example, if an appropriate value of t is not found, then the correction would fail. In a truncated (not primitive) code, an error location may be out of range. If the received vector has more errors than the code can correct, the decoder may unknowingly produce an apparently valid message that is not the one that was sent.

Calculate the syndromes

The received vector $R$ is the sum of the correct codeword $C$ and an unknown error vector $E.$ The syndrome values are formed by considering $R$ as a polynomial and evaluating it at $alpha^c,ldots,alpha^{c+d-2}.$ Thus the syndromes are

s_j = R(alpha^{j}) = C(alpha^{j}) + E(alpha^{j})

for $j = c$ to $c+d-2.$ Since $alpha^{j}$ are the zeros of $g(x),$ of which $C(x)$ is a multiple, $C(alpha^{j}) = 0.$ Examining the syndrome values thus isolates the error vector so one can begin to solve for it.

If there is no error, $s_j = 0$ for all $j.$ If the syndromes are all zero, then the decoding is done.

Calculate the error location polynomial

If there are nonzero syndromes, then there are errors. The decoder needs to figure out how many errors and the location of those errors.

If there is a single error, write this as $E(x) = e,x^i,$ where $i$ is the location of the error and $e$ is its magnitude. Then the first two syndromes are

s_c = e,alpha^{c,i}

s_{c+1} = e,alpha^{(c+1),i} = alpha^i s_c

so together they allow us to calculate $e$ and provide some information about $i$ (completely determining it in the case of Reed–Solomon codes).

If there are two or more errors,

E(x) = e_1 x^{i_1} + e_2 x^{i_2} + cdots ,

It is not immediately obvious how to begin solving the resulting syndromes for the unknowns $e_k$ and $i_k.$ First step is finding locator polynomial

Lambda(x)=prod_{j=1}^t (xalpha^{i_j}-1)

compatible with computed syndromes and with minimal possible

t.

Two popular algorithms for this task are:

Peterson–Gorenstein–Zierler algorithm

Peterson’s algorithm is the step 2 of the generalized BCH decoding procedure. Peterson’s algorithm is used to calculate the error locator polynomial coefficients $lambda_1 , lambda_2, dots, lambda_{v}$ of a polynomial

Lambda(x) = 1 + lambda_1 x + lambda_2 x^2 + cdots + lambda_v x^v .

Now the procedure of the Peterson–Gorenstein–Zierler algorithm. Expect we have at least 2t syndromes s_c,…,s_c+2t−1. Let v = t.

Start by generating the $S_{vtimes v}$ matrix with elements that are syndrome values

S_{v times v}=begin{bmatrix}s_c&s_{c+1}&dots&s_{c+v-1} s_{c+1}&s_{c+2}&dots&s_{c+v} vdots&vdots&ddots&vdots s_{c+v-1}&s_{c+v}&dots&s_{c+2v-2}end{bmatrix}.

Generate a $c_{v times 1}$ vector with elements

C_{v times 1}=begin{bmatrix}s_{c+v} s_{c+v+1} vdots s_{c+2v-1}end{bmatrix}.

Let $Lambda$ denote the unknown polynomial coefficients, which are given by

Lambda_{v times 1} = begin{bmatrix}lambda_{v} lambda_{v-1} vdots lambda_{1}end{bmatrix}.

Form the matrix equation

S_{v times v} Lambda_{v times 1} = -C_{v times 1,} .

If the determinant of matrix $S_{v times v}$ is nonzero, then we can actually find an inverse of this matrix and solve for the values of unknown $Lambda$ values.
If $det(S_{v times v}) = 0 ,$ then follow

if  $v = 0$  then declare an empty error locator polynomial stop Peterson procedure. end set  $v leftarrow v -1$  continue from the beginning of Peterson's decoding by making smaller  $S_{v times v}$

After you have values of $Lambda$ , you have with you the error locator polynomial.
Stop Peterson procedure.

Factor error locator polynomial

Now that you have the $Lambda(x)$ polynomial, its roots can be found in the form $Lambda(x)=(alpha^{i_1} x - 1) (alpha^{i_2} x - 1) cdots (alpha^{i_v} x - 1)$ by brute force for example using the Chien search algorithm. The exponential powers of the primitive element $alpha$ will yield the positions where errors occur in the received word; hence the name ‘error locator’ polynomial.

The zeros of Λ(x) are α^−i₁, …, α^−i_v.

Calculate error values

Once the error locations are known, the next step is to determine the error values at those locations. The error values are then used to correct the received values at those locations to recover the original codeword.

For the case of binary BCH, (with all characters readable) this is trivial; just flip the bits for the received word at these positions, and we have the corrected code word. In the more general case, the error weights $e_j$ can be determined by solving the linear system

begin{align} s_c & = e_1 alpha^{c,i_1} + e_2 alpha^{c,i_2} + cdots s_{c+1} & = e_1 alpha^{(c + 1),i_1} + e_2 alpha^{(c + 1),i_2} + cdots & {} vdots end{align}

Forney algorithm

However, there is a more efficient method known as the Forney algorithm.

Let

S(x)=s_c+s_{c+1}x+s_{c+2}x^2+cdots+s_{c+d-2}x^{d-2}.

vleqslant d-1, lambda_0neq 0 qquad Lambda(x)=sum_{i=0}^vlambda_ix^i=lambda_0 prod_{k=0}^{v} (alpha^{-i_k}x-1).

And the error evaluator polynomial

Omega(x) equiv S(x) Lambda(x) bmod{x^{d-1}}

Finally:

Lambda'(x) = sum_{i=1}^v i cdot lambda_i x^{i-1},

where

icdot x := sum_{k=1}^i x.

Than if syndromes could be explained by an error word, which could be nonzero only on positions $i_k$ , then error values are

e_k=-{alpha^{i_k}Omega(alpha^{-i_k})over alpha^{ccdot i_k}Lambda'(alpha^{-i_k})}.

For narrow-sense BCH codes, c = 1, so the expression simplifies to:

e_k=-{Omega(alpha^{-i_k})over Lambda'(alpha^{-i_k})}.

Explanation of Forney algorithm computation

It is based on and techniques of .

Consider $S(x)Lambda(x),$ and for the sake of simplicity suppose $lambda_k=0$ for $k>v,$ and $s_k=0$ for $k>c+d-2.$ Then

S(x)Lambda(x)=sum_{j=0}^{infty}sum_{i=0}^j s_{j-i+1}lambda_i x^j.

begin{align} S(x)Lambda(x) &=S(x) left { lambda_0prod_{ell=1}^v left (alpha^{i_ell}x-1 right ) right } &= left { sum_{i=0}^{d-2}sum_{j=1}^v e_jalpha^{(c+i)cdot i_j} x^i right } left { lambda_0prod_{ell=1}^v left (alpha^{i_ell}x-1 right ) right } &= left { sum_{j=1}^v e_j alpha^{c i_j}sum_{i=0}^{d-2} left (alpha^{i_j} right )^i x^i right } left { lambda_0prod_{ell=1}^v left (alpha^{i_ell}x-1 right ) right } &= left { sum_{j=1}^v e_j alpha^{c i_j} frac{left (x alpha^{i_j} right )^{d-1}-1}{x alpha^{i_j}-1} right } left { lambda_0 prod_{ell=1}^v left (alpha^{i_ell}x-1 right ) right } &= lambda_0 sum_{j=1}^v e_jalpha^{c i_j} frac{ left (xalpha^{i_j} right)^{d-1}-1}{xalpha^{i_j}-1} prod_{ell=1}^v left (alpha^{i_ell}x-1 right ) &=lambda_0 sum_{j=1}^v e_jalpha^{c i_j} left ( left (xalpha^{i_j} right)^{d-1}-1 right ) prod_{ellin{1,cdots,v}setminus{j}} left (alpha^{i_ell}x-1 right ) end{align}

We want to compute unknowns $e_j,$ and we could simplify the context by removing the $(xalpha^{i_j})^{d-1}$ terms. This leads to the error evaluator polynomial

Omega(x) equiv S(x) Lambda(x) bmod{x^{d-1}}.

Thanks to $vleqslant d-1$ we have

Omega(x) = -lambda_0sum_{j=1}^v e_jalpha^{c i_j} prod_{ellin{1,cdots,v}setminus{j}} left (alpha^{i_ell}x-1 right ).

Thanks to $Lambda$ (the Lagrange interpolation trick) the sum degenerates to only one summand for $x = alpha^{-i_k}$

Omega left (alpha^{-i_k} right )=-lambda_0e_kalpha^{ccdot i_k}prod_{ellin{1,cdots,v}setminus{k}} left (alpha^{i_ell}alpha^{-i_k}-1 right ).

To get $e_k$ we just should get rid of the product. We could compute the product directly from already computed roots $alpha^{-i_j}$ of $Lambda,$ but we could use simpler form.

Lambda'(x)=lambda_0sum_{j=1}^v alpha^{i_j}prod_{ellin{1,cdots,v}setminus{j}} left (alpha^{i_ell}x-1 right ),

we get again only one summand in

Lambda'(alpha^{-i_k})=lambda_0alpha^{i_k}prod_{ellin{1,cdots,v}setminus{k}} left (alpha^{i_ell}alpha^{-i_k}-1 right ).

So finally

e_k=- frac{alpha^{i_k}Omega left (alpha^{-i_k} right )}{alpha^{ccdot i_k}Lambda' left (alpha^{-i_k} right )}.

This formula is advantageous when one computes the formal derivative of $Lambda$ form

Lambda(x)=sum_{i=1}^vlambda_ix^i

yielding:

Lambda'(x) = sum_{i=1}^v i cdot lambda_i x^{i-1},

where

icdot x := sum_{k=1}^i x.

Decoding based on extended Euclidean algorithm

An alternate process of finding both the polynomial Λ and the error locator polynomial is based on Yasuo Sugiyama’s adaptation of the . Correction of unreadable characters could be incorporated to the algorithm easily as well.

Let $k_1, ... ,k_k$ be positions of unreadable characters. One creates polynomial localising these positions $Gamma(x)=prod_{i=1}^k(xalpha^{k_i}-1).$ Set values on unreadable positions to 0 and compute the syndromes.

As we have already defined for the Forney formula let $S(x)=sum_{i=0}^{d-2}s_{c+i}x^i.$

Let us run extended Euclidean algorithm for locating least common divisor of polynomials $S(x)Gamma(x)$ and $x^{d-1}.$ The goal is not to find the least common divisor, but a polynomial $r(x)$ of degree at most $lfloor (d+k-3)/2rfloor$ and polynomials $a(x), b(x)$ such that $r(x)=a(x)S(x)Gamma(x)+b(x)x^{d-1}.$ Low degree of $r(x)$ guarantees, that $a(x)$ would satisfy extended (by $Gamma$ ) defining conditions for $Lambda.$

Defining $Xi(x)=a(x)Gamma(x)$ and using $Xi$ on the place of $Lambda(x)$ in the Fourney formula will give us error values.

The main advantage of the algorithm is that it meanwhile computes $Omega(x)=S(x)Xi(x)bmod x^{d-1}=r(x)$ required in the Forney formula.

Explanation of the decoding process

The goal is to find a codeword which differs from the received word minimally as possible on readable positions. When expressing the received word as a sum of nearest codeword and error word, we are trying to find error word with minimal number of non-zeros on readable positions. Syndrom $s_i$ restricts error word by condition

s_i=sum_{j=0}^{n-1}e_jalpha^{ij}.

We could write these conditions separately or we could create polynomial

S(x)=sum_{i=0}^{d-2}s_{c+i}x^i

and compare coefficients near powers $0$ to $d-2.$

S(x) stackrel{{0,cdots,,d-2}}{=} E(x)=sum_{i=0}^{d-2}sum_{j=0}^{n-1}e_jalpha^{ij}alpha^{cj}x^i.

Suppose there is unreadable letter on position $k_1,$ we could replace set of syndromes ${s_c,cdots,s_{c+d-2}}$ by set of syndromes ${t_c,cdots,t_{c+d-3}}$ defined by equation $t_i=alpha^{k_1}s_i-s_{i+1}.$ Suppose for an error word all restrictions by original set ${s_c,cdots,s_{c+d-2}}$ of syndromes hold, than

t_i=alpha^{k_1}s_i-s_{i+1}=alpha^{k_1}sum_{j=0}^{n-1}e_jalpha^{ij}-sum_{j=0}^{n-1}e_jalpha^jalpha^{ij}=sum_{j=0}^{n-1}e_j(alpha^{k_1}-alpha^j)alpha^{ij}.

New set of syndromes restricts error vector

f_j=e_j(alpha^{k_1}-alpha^j)

the same way the original set of syndromes restricted the error vector $e_j.$ Note, that except the coordinate $k_1,$ where we have $f_{k_1}=0,$ an $f_j$ is zero, if $e_j = 0.$ For the goal of locating error positions we could change the set of syndromes in the similar way to reflect all unreadable characters. This shortens the set of syndromes by $k.$

In polynomial formulation, the replacement of syndromes set ${s_c,cdots,s_{c+d-2}}$ by syndromes set ${t_c,cdots,t_{c+d-3}}$ leads to

T(x)=sum_{i=0}^{d-3}t_{c+i}x^i=alpha^{k_1}sum_{i=0}^{d-3}s_{c+i}x^i-sum_{i=1}^{d-2}s_{c+i}x^{i-1}.

Therefore,

xT(x) stackrel{{1,cdots,,d-2}}{=} left (xalpha^{k_1}-1 right )S(x).

After replacement of $S(x)$ by $S(x)Gamma(x)$ , one would require equation for coefficients near powers $k,cdots,d-2.$

One could consider looking for error positions from the point of view of eliminating influence of given positions similarly as for unreadable characters. If we found $v$ positions such that eliminating their influence leads to obtaining set of syndromes consisting of all zeros, than there exists error vector with errors only on these coordinates. If $Lambda(x)$ denotes the polynomial eliminating the influence of these coordinates, we obtain

S(x)Gamma(x)Lambda(x) stackrel{{k+v,cdots, d-2}}{=} 0.

In Euclidean algorithm, we try to correct at most $tfrac{1}{2}(d-1-k)$ errors (on readable positions), because with bigger error count there could be more codewords in the same distance from the received word. Therefore, for $Lambda(x)$ we are looking for, the equation must hold for coefficients near powers starting from

k+ left lfloor tfrac{1}{2} (d-1-k) right rfloor.

In Forney formula, $Lambda(x)$ could be multiplied by a scalar giving the same result.

It could happen that the Euclidean algorithm finds $Lambda(x)$ of degree higher than $tfrac{1}{2}(d-1-k)$ having number of different roots equal to its degree, where the Fourney formula would be able to correct errors in all its roots, anyway correcting such many errors could be risky (especially with no other restrictions on received word). Usually after getting $Lambda(x)$ of higher degree, we decide not to correct the errors. Correction could fail in the case $Lambda(x)$ has roots with higher multiplicity or the number of roots is smaller than its degree. Fail could be detected as well by Forney formula returning error outside the transmitted alphabet.

Correct the errors

Using the error values and error location, correct the errors and form a corrected code vector by subtracting error values at error locations.

Decoding examples

Decoding of binary code without unreadable characters

Consider a BCH code in GF(2⁴) with $d=7$ and $g(x) = x^{10} + x^8 + x^5 + x^4 + x^2 + x + 1$ . (This is used in .) Let the message to be transmitted be [1 1 0 1 1], or in polynomial notation, $M(x) = x^4 + x^3 + x + 1.$ The “checksum” symbols are calculated by dividing $x^{10} M(x)$ by $g(x)$ and taking the remainder, resulting in $x^9 + x^4 + x^2$ or [ 1 0 0 0 0 1 0 1 0 0 ]. These are appended to the message, so the transmitted codeword is [ 1 1 0 1 1 1 0 0 0 0 1 0 1 0 0 ].

Now, imagine that there are two bit-errors in the transmission, so the received codeword is [ 1 0 1 1 1 0 0 0 1 0 1 0 0 ]. In polynomial notation:

R(x) = C(x) + x^{13} + x^5 = x^{14} + x^{11} + x^{10} + x^9 + x^5 + x^4 + x^2

In order to correct the errors, first calculate the syndromes. Taking $alpha = 0010,$ we have $s_1 = R(alpha^1) = 1011,$ $s_2 = 1001,$ $s_3 = 1011,$ $s_4 = 1101,$ $s_5 = 0001,$ and $s_6 = 1001.$ Next, apply the Peterson procedure by row-reducing the following augmented matrix.

left [ S_{3 times 3} | C_{3 times 1} right ] = begin{bmatrix}s_1&s_2&s_3&s_4 s_2&s_3&s_4&s_5 s_3&s_4&s_5&s_6end{bmatrix} = begin{bmatrix}1011&1001&1011&1101 1001&1011&1101&0001 1011&1101&0001&1001end{bmatrix} Rightarrow begin{bmatrix}0001&0000&1000&0111 0000&0001&1011&0001 0000&0000&0000&0000end{bmatrix}

Due to the zero row, is singular, which is no surprise since only two errors were introduced into the codeword. However, the upper-left corner of the matrix is identical to , which gives rise to the solution $lambda_2 = 1000,$ $lambda_1 = 1011.$ The resulting error locator polynomial is $Lambda(x) = 1000 x^2 + 1011 x + 0001,$ which has zeros at $0100 = alpha^{-13}$ and $0111 = alpha^{-5}.$ The exponents of $alpha$ correspond to the error locations. There is no need to calculate the error values in this example, as the only possible value is 1.

Decoding with unreadable characters

Suppose the same scenario, but the received word has two unreadable characters [ 1 0 ? 1 1 ? 0 0 1 0 1 0 0 ]. We replace the unreadable characters by zeros while creating the polynom reflecting their positions $Gamma(x)=(alpha^8x-1)(alpha^{11}x-1).$ We compute the syndromes $s_1=alpha^{-7}, s_2=alpha^{1}, s_3=alpha^{4}, s_4=alpha^{2}, s_5=alpha^{5},$ and $s_6=alpha^{-7}.$ (Using log notation which is independent on GF(2⁴) isomorphisms. For computation checking we can use the same representation for addition as was used in previous example. Hexadecimal description of the powers of $alpha$ are consecutively 1,2,4,8,3,6,C,B,5,A,7,E,F,D,9 with the addition based on bitwise xor.)

Let us make syndrome polynomial

S(x)=alpha^{-7}+alpha^{1}x+alpha^{4}x^2+alpha^{2}x^3+alpha^{5}x^4+alpha^{-7}x^5,

compute

S(x)Gamma(x)=alpha^{-7}+alpha^{4}x+alpha^{-1}x^2+alpha^{6}x^3+alpha^{-1}x^4+alpha^{5}x^5+alpha^{7}x^6+alpha^{-3}x^7.

Run the extended Euclidean algorithm:

begin{align} begin{pmatrix}S(x)Gamma(x)\ x^6end{pmatrix} &= begin{pmatrix}alpha^{-7} +alpha^{4}x+ alpha^{-1}x^2+ alpha^{6}x^3+ alpha^{-1}x^4+alpha^{5}x^5 +alpha^{7}x^6+ alpha^{-3}x^7 \ x^6end{pmatrix} \ [6pt] &=begin{pmatrix}alpha^{7}+alpha^{-3}x&1\ 1&0end{pmatrix} begin{pmatrix}x^6\ alpha^{-7} +alpha^{4}x +alpha^{-1}x^2 +alpha^{6}x^3 +alpha^{-1}x^4 +alpha^{5}x^5 +2alpha^{7}x^6 +2alpha^{-3}x^7end{pmatrix} \ [6pt] &=begin{pmatrix}alpha^{7}+alpha^{-3}x&1\ 1&0end{pmatrix} begin{pmatrix}alpha^4+alpha^{-5}x&1\ 1&0end{pmatrix} times &qquad times begin{pmatrix} alpha^{-7}+alpha^{4}x+alpha^{-1}x^2+alpha^{6}x^3+alpha^{-1}x^4+alpha^{5}x^5\ alpha^{-3} +(alpha^{-7}+alpha^{3})x+(alpha^{3}+alpha^{-1})x^2+(alpha^{-5}+alpha^{-6})x^3+(alpha^3+alpha^{1})x^4+ 2alpha^{-6}x^5+ 2x^6end{pmatrix} \ [6pt] &=begin{pmatrix}(1+alpha^{-4})+(alpha^{1}+alpha^{2})x+alpha^{7}x^2&alpha^{7}+alpha^{-3}x \ alpha^4+alpha^{-5}x&1end{pmatrix} begin{pmatrix} alpha^{-7} +alpha^{4}x +alpha^{-1}x^2+ alpha^{6}x^3+alpha^{-1}x^4+alpha^{5}x^5\ alpha^{-3}+alpha^{-2}x+alpha^{0}x^2+ alpha^{-2}x^3+alpha^{-6}x^4end{pmatrix} \ [6pt] &=begin{pmatrix}alpha^{-3}+alpha^{5}x+alpha^{7}x^2&alpha^{7}+alpha^{-3}x \ alpha^4+alpha^{-5}x&1end{pmatrix} begin{pmatrix}alpha^{-5}+alpha^{-4}x&1\ 1&0 end{pmatrix} times &qquad times begin{pmatrix} alpha^{-3}+alpha^{-2}x+alpha^{0}x^2+ alpha^{-2}x^3+alpha^{-6}x^4\ (alpha^{7}+alpha^{-7})+ (2alpha^{-7}+alpha^{4})x+ (alpha^{-5}+alpha^{-6}+alpha^{-1})x^2+ (alpha^{-7}+alpha^{-4}+alpha^{6})x^3+ (alpha^{4}+alpha^{-6}+alpha^{-1})x^4+ 2alpha^{5}x^5end{pmatrix} \ [6pt] &=begin{pmatrix} alpha^{7}x+alpha^{5}x^2+alpha^{3}x^3&alpha^{-3}+alpha^{5}x+alpha^{7}x^2\ alpha^{3}+alpha^{-5}x+alpha^{6}x^2&alpha^4+alpha^{-5}xend{pmatrix} begin{pmatrix} alpha^{-3}+alpha^{-2}x+alpha^{0}x^2+ alpha^{-2}x^3+alpha^{-6}x^4\ alpha^{-4}+alpha^{4}x+alpha^{2}x^2+ alpha^{-5}x^3end{pmatrix}. end{align}

We have reached polynomial of degree at most 3, and as

begin{pmatrix}-(alpha^4+alpha^{-5}x)&alpha^{-3}+alpha^{5}x+alpha^{7}x^2\ alpha^{3}+alpha^{-5}x+alpha^{6}x^2&-(alpha^{7}x+alpha^{5}x^2+alpha^{3}x^3)end{pmatrix} begin{pmatrix} alpha^{7}x+alpha^{5}x^2+alpha^{3}x^3&alpha^{-3}+alpha^{5}x+alpha^{7}x^2\ alpha^{3}+alpha^{-5}x+alpha^{6}x^2&alpha^4+alpha^{-5}xend{pmatrix} =begin{pmatrix}1&0\ 0&1end{pmatrix},

we get

begin{pmatrix}-(alpha^4+alpha^{-5}x)&alpha^{-3}+alpha^{5}x+alpha^{7}x^2\ alpha^{3}+alpha^{-5}x+alpha^{6}x^2&-(alpha^{7}x+alpha^{5}x^2+alpha^{3}x^3)end{pmatrix} begin{pmatrix}S(x)Gamma(x)\ x^6end{pmatrix}= begin{pmatrix} alpha^{-3}+alpha^{-2}x+alpha^{0}x^2+alpha^{-2}x^3+alpha^{-6}x^4\ alpha^{-4}+alpha^{4}x +alpha^{2}x^2+alpha^{-5}x^3 end{pmatrix}.

Therefore,

S(x)Gamma(x)(alpha^{3}+alpha^{-5}x+alpha^{6}x^2)- (alpha^{7}x+alpha^{5}x^2+alpha^{3}x^3)x^6= alpha^{-4}+alpha^{4}x+alpha^{2}x^2+alpha^{-5}x^3.

Let $Lambda(x)=alpha^{3}+alpha^{-5}x+alpha^{6}x^2.$ Don’t worry that $lambda_0neq 1.$ Find by brute force a root of $Lambda.$ The roots are $alpha^2,$ and $alpha^{10}$ (after finding for example $alpha^2$ we can divide $Lambda$ by corresponding monom $(x-alpha^2)$ and the root of resulting monom could be found easily).

Let

Xi(x)=Gamma(x)Lambda(x)=alpha^3+alpha^4x^2+alpha^2x^3+alpha^{-5}x^4

Omega(x)=S(x)Xi(x) equiv alpha^{-4}+alpha^4x+alpha^2x^2+alpha^{-5}x^3 bmod{x^6}

Let us look for error values using formula

e_j=-frac{Omega left (alpha^{-i_j} right )}{Xi' left (alpha^{-i_j} right )},

where $alpha^{-i_j}$ are roots of $Xi(x).$ $Xi'(x)=alpha^{2}x^2.$ We get

begin{align} e_1 &=-frac{Omega(alpha^4)}{Xi'(alpha^{4})} =frac{alpha^{-4}+alpha^{-7}+alpha^{-5}+alpha^{7}}{alpha^{-5}} =frac{alpha^{-5}}{alpha^{-5}}=1 e_2 &=-frac{Omega(alpha^7)}{Xi'(alpha^{7})}=frac{alpha^{-4}+alpha^{-4}+alpha^{1}+alpha^{1}}{alpha^{1}}=0 e_3 &=-frac{Omega(alpha^{10})}{Xi'(alpha^{10})}=frac{alpha^{-4}+alpha^{-1}+alpha^{7}+alpha^{-5}}{alpha^{7}}=frac{alpha^{7}}{alpha^{7}}=1 e_4 &=-frac{Omega(alpha^{2})}{Xi'(alpha^{2})}=frac{alpha^{-4}+alpha^{6}+alpha^{6}+alpha^{1}}{alpha^{6}}=frac{alpha^{6}}{alpha^{6}}=1 end{align}

Fact, that $e_3=e_4=1,$ should not be surprising.

Corrected code is therefore [ 1 0 1 1 0 0 1 0 1 0 0].

Decoding with unreadable characters with a small number of errors

Let us show the algorithm behaviour for the case with small number of errors. Let the received word is [ 1 0 ? 1 1 ? 0 0 0 1 0 1 0 0 ].

Again, replace the unreadable characters by zeros while creating the polynom reflecting their positions $Gamma(x)=(alpha^8x-1)(alpha^{11}x-1).$ Compute the syndromes $s_1=alpha^{4}, s_2=alpha^{-7}, s_3=alpha^{1}, s_4=alpha^{1}, s_5=alpha^{0},$ and $s_6=alpha^{2}.$ Create syndrome polynomial

S(x)=alpha^{4}+alpha^{-7}x+alpha^{1}x^2+alpha^{1}x^3+alpha^{0}x^4+alpha^{2}x^5,

S(x)Gamma(x)=alpha^{4}+alpha^{7}x+alpha^{5}x^2+alpha^{3}x^3+alpha^{1}x^4+alpha^{-1}x^5+alpha^{-1}x^6+alpha^{6}x^7.

Let us run the extended Euclidean algorithm:

$begin{align} begin{pmatrix}S(x)Gamma(x)\ x^6end{pmatrix} &= begin{pmatrix} alpha^{4}+alpha^{7}x+alpha^{5}x^2 +alpha^{3}x^3+alpha^{1}x^4+alpha^{-1}x^5 +alpha^{-1}x^6+alpha^{6}x^7\ x^6end{pmatrix} &=begin{pmatrix}alpha^{-1}+alpha^{6}x&1\ 1&0end{pmatrix} begin{pmatrix}x^6\ alpha^{4}+alpha^{7}x+alpha^{5}x^2+alpha^{3}x^3+alpha^{1}x^4+alpha^{-1}x^5+2alpha^{-1}x^6+2alpha^{6}x^7 end{pmatrix} &=begin{pmatrix}alpha^{-1}+alpha^{6}x&1\ 1&0end{pmatrix} begin{pmatrix}alpha^{3}+alpha^{1}x&1\ 1&0end{pmatrix} begin{pmatrix} alpha^{4} +alpha^{7}x+ alpha^{5}x^2 +alpha^{3}x^3+alpha^{1}x^4+alpha^{-1}x^5\ alpha^{7}+(alpha^{-5}+alpha^{5})x+ 2alpha^{-7}x^2+2alpha^{6}x^3+ 2alpha^{4}x^4+ 2alpha^{2}x^5+ 2x^6 end{pmatrix} &=begin{pmatrix}(1+alpha^{2})+(alpha^{0}+alpha^{-6})x+alpha^{7}x^2&alpha^{-1}+alpha^{6}x\ alpha^{3}+alpha^{1}x&1end{pmatrix} begin{pmatrix} alpha^{4}+alpha^{7}x+ alpha^{5}x^2 +alpha^{3}x^3+ alpha^{1}x^4+alpha^{-1}x^5\ alpha^{7}+alpha^{0}x end{pmatrix} end{align}$

We have reached polynomial of degree at most 3, and as

begin{pmatrix}-1&alpha^{-1}+alpha^{6}x alpha^{3}+alpha^{1}x&-(alpha^{-7}+alpha^{7}x+alpha^{7}x^2)end{pmatrix} begin{pmatrix}alpha^{-7}+alpha^{7}x+alpha^{7}x^2&alpha^{-1}+alpha^{6}x alpha^{3}+alpha^{1}x&1end{pmatrix} =begin{pmatrix}1&0\ 0&1end{pmatrix},

we get

begin{pmatrix}-1&alpha^{-1}+alpha^{6}x alpha^{3}+alpha^{1}x&-(alpha^{-7}+alpha^{7}x+alpha^{7}x^2)end{pmatrix} begin{pmatrix}S(x)Gamma(x)\ x^6end{pmatrix}= begin{pmatrix}alpha^{4}+alpha^{7}x+alpha^{5}x^2+alpha^{3}x^3+alpha^{1}x^4+alpha^{-1}x^5 alpha^{7}+alpha^{0}x end{pmatrix}.

Therefore,

S(x)Gamma(x)(alpha^{3}+alpha^{1}x)- (alpha^{-7}+alpha^{7}x+alpha^{7}x^2)x^6= alpha^{7}+alpha^{0}x.

Let $Lambda(x)=alpha^{3}+alpha^{1}x.$ Don’t worry that $lambda_0neq 1.$ The root of $Lambda(x)$ is $alpha^{3-1}.$

Let

Xi(x)=Gamma(x)Lambda(x)=alpha^{3}+alpha^{-7}x+alpha^{-4}x^2+alpha^{5}x^3,

Omega(x)=S(x)Xi(x) equiv alpha^{7}+alpha^{0}x bmod{x^6}

Let us look for error values using formula $e_j=-Omega(alpha^{-i_j})/Xi'(alpha^{-i_j}),$ where $alpha^{-i_j}$ are roots of polynomial $Xi(x).$ $Xi'(x)=alpha^{-7}+alpha^{5}x^2.$ We get

begin{align} e_1 &=-frac{Omega(alpha^4)}{Xi'(alpha^{4})}=frac{alpha^{7}+alpha^{4}}{alpha^{-7}+alpha^{-2}}= frac{alpha^{3}}{alpha^{3}}=1 e_2 &=-frac{Omega(alpha^7)}{Xi'(alpha^{7})}=frac{alpha^{7}+alpha^{7}}{alpha^{-7}+alpha^{4}}= 0 e_3 &=-frac{Omega(alpha^2)}{Xi'(alpha^2)}= frac{alpha^{7}+alpha^{2}}{alpha^{-7}+alpha^{-6}}=frac{alpha^{-3}}{alpha^{-3}}=1 end{align}

The fact that $e_3=1$ should not be surprising.

Corrected code is therefore [ 1 0 1 1 0 0 0 1 0 1 0 0].

Citations

Source

http://wikipedia.org/

BCH code

Contents

General BCH codes

Special cases

Properties

Encoding

Decoding

Calculate the syndromes

Calculate the error location polynomial

Peterson–Gorenstein–Zierler algorithm

Factor error locator polynomial

Calculate error values

Forney algorithm

Explanation of Forney algorithm computation

Decoding based on extended Euclidean algorithm

Explanation of the decoding process

Correct the errors

Decoding examples

Decoding of binary code without unreadable characters

Decoding with unreadable characters

Decoding with unreadable characters with a small number of errors

Citations

Source

See Also on BitcoinWiki