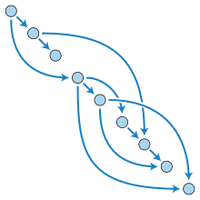
DAG
Directed Acyclic Graph is a directed graph that has a topological ordering, a sequence of the vertices such that every edge is directed earlier to later in the sequence.
Contents
DAG definition
Directed Acyclic Graph is a concept of a finite directed graph with no directed cycles. DAG definition is easier to understand if split in two parts.
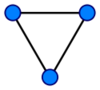
First of all, let’s talk about a “directed” part. Directed graph (digraph) is a multigraph which edges are assigned a direction. Directed edges are referred to as arcs, and in some sources, just edges. For the better understanding, let’s look at the examples:
1)  2)
2) 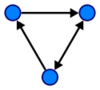
The example number one is an undirected graph. It shows that there is a connection between the vertices but does not provide it with the direction. Vertices are connected without an orientation. The graph number two is a directed graph as its connections have a direction. Sometimes, directed graph is referred to as oriented, but it is not a correct reference.
An oriented graph is a digraph without multiple edges or loops. Basically, it can be built by assigning one-way directions to the connections of a simple undirected graph. However, it can have a loop within its structure between more than two vertices. The example number two given earlier represents an oriented graph.
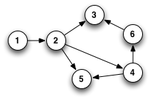
Again, let’s look at the examples. These are a little more complicated:
3)  4)
4) 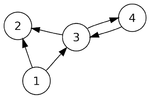
Both examples are directed graphs. However, only the graph number 3 is an oriented graph, as it contains no loops between two vertices and multiple edges. The graph number 4 has a 3-4 and 4-3 connections that represent a loop between the vertex 3 and the vertex 4.
Secondly, let’s talk about the “Acyclic” part of the definition. An acyclic graph is a digraph in which there are no directed loops, but there can be “parallel” paths coming from one node and different paths coming to the final node. It means that in the acyclic graph there is no way to start in the point a and to get back to the point a after a number of movements.
5)
Example 5 is a DAG. IT has no loops and has several parallel ways (B-D-E, B-C-E, B-E). One can’t find a way to start at any vertex of the graph and get back to it after any number of actions.
DAG has a parallel concept in the field of undirected graphs. It is called a tree and is an undirected graph without cycles, meaning there is only one path connecting 2 vertices in the graph. The example number one in this article is an undirected graph with cycles. The example of the tree is the following graph number 6:
6)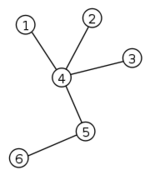
As you can see, it has no 2 vertices connected with more than one path. Because of the existence of the tree, directed acyclic graphs are mostly referred to in full name (not just “acyclic graph”).
DAGs are a very important part of the whole IT industry and the cryptocurrency industry in particular. They are widely implemented in AI development, statistics and machine learning. They were also implemented in several hashing functions and became a powerful force behind some blockchain-based networks.
DAGs are used in math and IT for modeling different things. For example, one can model a spreadsheet by assigning a vertex for each cell and an edge whenever the formula in one cell uses the value from another. Similar implementations can be used in logistics, cryptography, dataflow programming amongst other things.
DAG implementations
Directed acyclic graphs can represent various things and are widely implemented to model processes and objects. The example of the spreadsheet modelling was given earlier but is far from being an only application of the DAG.
One implementation case can be a scheduling problem. Scheduling is a long-time math problem that was approached by various fields of science. Directed acyclic graphs come in handy when we are talking about the processes that have a strict order and are not performed in loops. From this point of view, DAGs can be implemented in the product management, project management and similar fields of work. This management techniques for the human-driven processes vertices represent turning points of the project and the edges represent the activity that is necessary to get to the turning point. This approach is used because routine everyday work is often done in loops. However, milestones of the project are reached only once, which makes it acceptable for the implementation of the DAG.
DAGs are useful to represent a data flow. It can be used both for the development of the generation process of the data and to build a data processing network. In this case, data is going by the edges through the vertices transforming alongside some encoded protocols. This approach is used on the dataflow programming languages, electronic circuit design and some other technologies.
We wouldn’t linger on the other implementations but will mention them. Directed Acyclic Graphs are implemented in genealogy, causal structures, citation graphs and data compression. This wide range of cases makes DAGs important in many various science fields like history, cryptography, data science, sociology and others.
DAG and cryptocurrency
DAGs are used in the development of encryption techniques and hashing functions. Probably, the most notable implementation of DAG in the cryptocurrency industry is in the Dagger algorithm by Vitalik Buterin. According to the whitepaper of the algorithm, Dagger operates by creating a directed acyclic graph (a tree where each node is allowed to have multiple parents) with ten levels including the root and a total of 225 – 1 values. Dagger was later implemented in the Dagger-Hashimoto algorithm and the Ethash algorithm.
DAGs are also used in the cryptocurrency industry to provide a blockchain-like structures as an alternative to blockchain itself or as a part of structure within it. The Nano (NANO) cryptocurrency is the example of DAG implementation. It is a low-latency payment network built upon a DAG architecture. The network of Nano provides users with their blockchains in their accounts and connects them along the DAG-structured network.
Another example of the DAG usage in cryptocurrency development is Byteball Bytes (GBYTE). This cryptocurrency stores and ordering the data using a directed acyclic graph. Because of the strict ordering structure of the GBYTE network, users can secure each other’s data by referencing earlier data units created by other users. It also helps to deal with scalability issues that are inherent to the blockchain technology.
IOTA is also a cryptocurrency with an implementation of DAG in its structure. IOTA is established based on the Tangle technology. The Tangle is the data structure uses a DAG instead of a blockchain to store the ledger of IOTA. Because of the IOTA’s goal is to be a platform for machine-to-machine communication, blockchain structure is not scalable enough to be a foundation for it. The Tangle is a solution that represents a DAG where vertices represent transactions, and edges represent approvals. New transactions are added as new vertices.
See Also on BitcoinWiki
Resources
- Wikipedia: Graph (discrete mathematics)
- Wikipedia: Oriented Graph (In Russian)
- Wolfram platform: Oriented graph
- Wikipedia: Directed acyclic graph
- StackExchange Oriented graph vs directed graph topic
- Coinbureau: Everything You Need to Know About Directed Acyclic Graphs (DAGS)
- Byteball website
- Nano website: about
- Dzone: Introduction to DAG and Blockchain-less Cryptocurrencies
- IOTA: Meet the tangle